Sabemos que elétrons, núcleos, moléculas, engrenagens, polias, estrelas, planetas e galáxias, todos giram. Mas você já se perguntou o que os fazem girar? Uma vez girando o que os fazem parar?
A resposta para essas perguntas está diretamente relacionada com o torque, que carreta uma variação de velocidade vetorial angular dos corpos, bem como uma força modifica a velocidade vetorial linear de um objeto.

No movimento de rotação observamos que os corpos podem girar em diversas situações, por exemplo quando temos dois objetos acoplados, engrenagens. Esses passam a girar em sentidos opostos , como se o giro de um buscasse compensar o giro do outro.
Analisando essa situação e fazendo uma analogia com o movimento de translação, no movimento de rotação há algo que não varia que denominamos momento angular.
Na página momento de inércia vimos que um corpo que está girando pode ter sua velocidade alterada se o momento de inércia do corpo for alterado, por exemplo: imagine um atleta de salto olímpico, que ao executar um salto tem necessidade de encolher os braços e pernas. Você já parou para pensar por que ele faz isso?
A resposta é ao saltar do trampolim, o atleta adquire uma velocidade de rotação em torno do eixo perpendicular ao plano do movimento (esse eixo passa por um ponto, no qual, pode -se considerar que toda massa do corpo está ali concentrada, denominada centro de massa).

Ao encolher os braços o momento de inércia diminui e sua velocidade de rotação aumenta. Tal efeito é garantido pela conservação do momento angular que será discutido mais adiante.
Assim podemos escrever a equação do momento angular como:
![]()
sendo sua unidade ![]() .
.
A equação mostra que o momento angular além de depender da velocidade angular possui mesma direção e sentido da velocidade angular que podem ser definidos pela regra da mão direita.
Desenvolvendo a equação do momento angular e considerando o momento de inércia para uma partícula ![]() e velocidade angular
e velocidade angular ![]() temos:
temos:
![]()
Lembrando que o momento linear é ![]() temos que:
temos que:
![]()
ou seja, o momento angular depende do momento linear, onde ![]() é o vetor posição da partícula em relação à origem
é o vetor posição da partícula em relação à origem ![]() e
e ![]() é o vetor momento linear de uma partícula situada em um ponto dista
é o vetor momento linear de uma partícula situada em um ponto dista ![]() em relação a origem
em relação a origem ![]() .
.
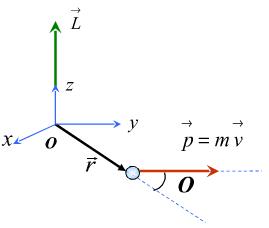
Então podemos definir o momento angular como:
O vetor momento angular![]() é paralelo ao eixo z e aponta no sentido crescente de z. Assim
é paralelo ao eixo z e aponta no sentido crescente de z. Assim ![]() é positivo em concordância com a rotação no sentido anti – horário executado pelo vetor
é positivo em concordância com a rotação no sentido anti – horário executado pelo vetor ![]() em torno do eixo z.
em torno do eixo z.
O módulo de ![]() pode ser determinado pela análise dos vetores
pode ser determinado pela análise dos vetores ![]() e
e ![]() , considerando sempre que
, considerando sempre que ![]() e
e ![]() são perpendiculares.
são perpendiculares.
![]()
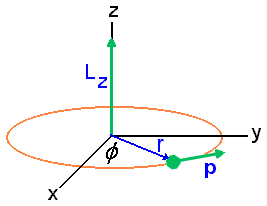
Considerando o ângulo ![]() entre
entre ![]() e
e ![]() temos que
temos que ![]() temos que
temos que ![]() . Então podemos escrever o módulo de
. Então podemos escrever o módulo de ![]() como:
como:
![]()
Podemos ver então que se o momento angular depende da velocidade linear e da distância do corpo até o eixo de rotação, ou seja, o raio.
Na simulação a seguir é possível verificar a relação entre essas três grandezas.

2ª Lei de Newton no movimento de rotação
Na página torque, vimos que o torque no movimento de rotação é análogo à força no movimento de translação. Assim pensando nos momentos podemos fazer a seguinte relação:
- no movimento de translação:
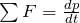
- no movimento de rotação:
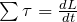
Conservação do Momento Angular
Você já deve ter observado o movimento de pião girando, uma bailarina rodopiando ou até mesmo um atleta saltando em uma piscina que gira durante a queda. Porém você já se perguntou como a velocidade desses giros são variadas? Então nesta seção iremos apresentar porque a velocidade das rotações são alteradas e quais condições são necessárias.
Já discutimos anteriormente a conservação da energia e momento linear. Apresentaremos agora a conservação do momento angular. Primeiramente vamos lembrar a condição para a conservação do momento linear que é determinada por ![]() , então analogamente temos que:
, então analogamente temos que:
![]()
Isso significa que se nenhum torque resultante atuar sobre o corpo, o momento angular será conservado.
O torque resultante sobre um sistema é zero em duas situações: quando a força resultante sobre o sistema é zero e quando a força que atua sobre o sistema é central.
Começaremos a discutir o caso quando a força resultante é zero com o exemplo que chamamos de pião humano.
Imagine uma pessoa sentada em um banco que pode girar livremente em torno do eixo vertical. A pessoa segura dois alteres com os braços abertos, quando sofre ação de uma força, adquirindo uma velocidade angular ![]() .
.
A animação a seguir mostra que quando a pessoa fecha os braços sua velocidade angular é alterada, a pessoa passa girar mais rápido.

Mas por que isso acontece? A soma das forças, força peso e força que a superfície exerce sobre o banco, que atuam sobre o sistema (pessoa, halteres e banco) é zero, assim o torque resultante sobre o sistema também é zero, o que resulta na conservação do momento angular.
Assim quando a pessoa fecha os braços o momento de inércia do sistema diminui de ![]() para
para ![]() e sua velocidade angular aumenta
e sua velocidade angular aumenta ![]() para
para ![]() , garantindo a conservação do momento angular.
, garantindo a conservação do momento angular.
Na figura a seguir podemos identificar o vetor do momento angular.
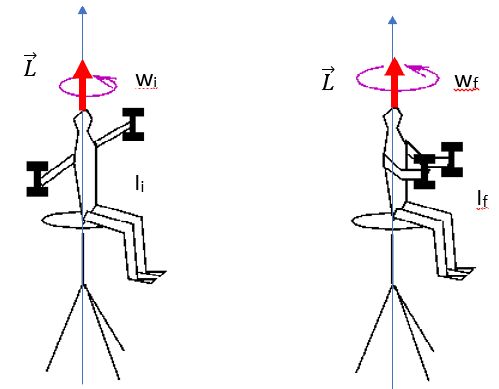
A direção e sentido da velocidade são determinadas pela regra da mão direita.
Equacionando o problema temos:
![]()
Podemos aplicar essa mesma análise para uma bailarina que rodopia. Ao fechar os braços sua velocidade angular aumenta porque seu momento de inércia diminui.

Voltemos no exemplo da pessoa sentada no banco que gira livremente. Agora ela segura uma haste que tem em uma de suas extremidades uma roda que gira livremente, de forma que o eixo de rotação da roda é perpendicular ao eixo de rotação do banco. De repente a a pessoa gira a roda de forma que os eixos de rotação fiquem paralelos, o que será que irá acontecer?

O vídeo mostra que quando os eixos são perpendiculares a pessoa permanece parado, porém quando os eixos são colocados em paralelo, a pessoa se movimenta em sentido oposto ao da roda.
Quando a roda é colocada na horizontal não há momento na vertical e por isso a pessoa juntamente com o banco permanecem parados.
A roda possui momento angular inicial que chamaremos de ![]() . Quando a roda é colocada na vertical para cima a pessoa começa a girar em sentido oposto com um momento angular em sentido oposto ao da roda como mostra a figura.
. Quando a roda é colocada na vertical para cima a pessoa começa a girar em sentido oposto com um momento angular em sentido oposto ao da roda como mostra a figura.
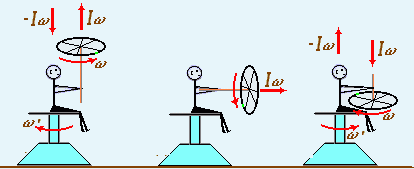
De acordo com a conservação do momento angular podemos escrever:
![]()
Isso mostra que a roda e conjunto possuem a mesma velocidade porém estão em sentidos opostos.
Quando a pessoa coloca o roda na vertical na parte inferior, o sentido no momento angular inverte, mas sua direção é a mesma. Considerando a conservação do momento angular, temos que a o momento inicial deve ser mesmo em qualquer situação. Assim quando a roda está na parte inferior temos:
![]()
O resultado mostra que o sistema (banco + pessoa) irão girar com o dobro da velocidade da roda e em sentido oposto a essa.
Vamos pensar em outro exemplo. Todos nós sabemos que de acordo com a 1ª de Lei de Newton um corpo tende a permanecer em repouso ou movimento retilíneo uniforme quando a força resultante sobre ele é zero. É por isso que uma nave espacial permanece em movimento no espaço sem os motores ligados. Mas se quisermos mudar a direção o que devemos fazer?
Imagine um veículo espacial dotado de um volante firmemente preso à sua estrutura.
Para mudar a direção do veículo espacial, o volante é acionado e o veículo começa a girar em sentido oposto ao do volante para manter nulo o momento angular do sistema. Quando o volante retorna ao repouso, o veículo também deixará de girar, mas sua orientação terá mudado.
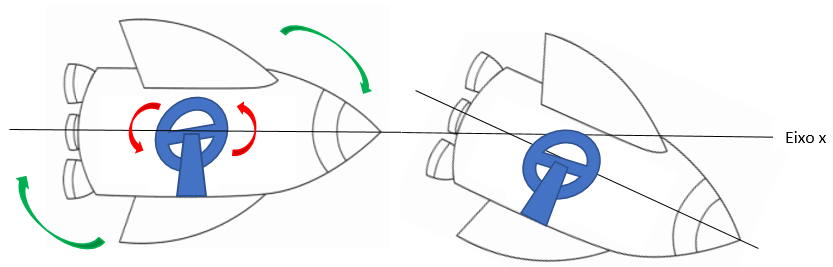
O conjunto (veículo + volante) formam um sistema isolado e possuem momento angular zero que deverá permanecer sempre em qualquer situação de acordo com a lei da conservação.
Explicar o movimento do pião e do giroscópio
Conservação do momento angular e forças centrais
Vimos anteriormente que para o momento angular ser conservado é necessário que o torque resultante seja zero, que é obtido por meio da força resultante igual a zero. Mas se a força resultante não for zero é possível termos um torque resultante igual a zero e consequentemente a conservação do momento angular?
A resposta é sim. Para isso acontecer o torque deve deve ser medido em relação a um ponto contido na linha de ação da força resultante. Podemos citar como exemplo, o torque sobre um planeta, em relação ao Sol, devido à força gravitacional do Sol sobre o planeta.
Consideremos um planeta de massa ![]() em órbita elíptica em torno do Sol, como mostra a figura a seguir.
em órbita elíptica em torno do Sol, como mostra a figura a seguir.
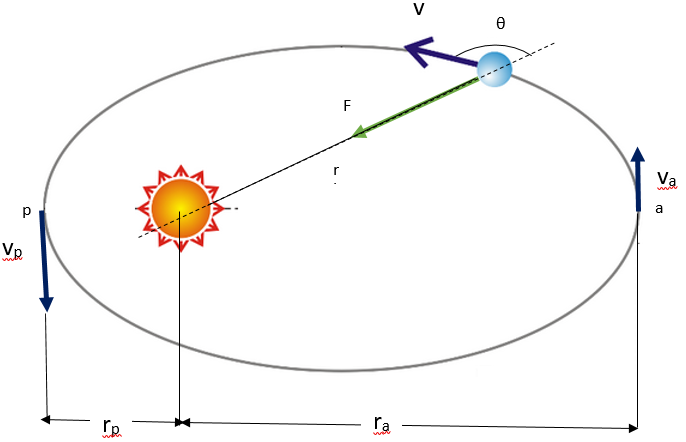
Iremos tomar como sistema apenas o planeta (excluindo o Sol). A força gravitacional sobre o planeta devida ao Sol é dirigida diretamente para o Sol. O braço momento desta força em relação á posição do Sol é zero, de modo que o torque em relação ao Sol devido a esta força é zero.
Temos então:
Se o torque é ![]() e o ângulo entre o vetor
e o ângulo entre o vetor ![]() e o vetor
e o vetor ![]() é zero, temos que
é zero, temos que ![]() , então
, então ![]()
Portanto, o momento angular orbital do planeta em torno do Sol é constante, isto é, conservado.
![]()
Todas as três grandezas ![]() ,
, ![]() e
e ![]() , variam com o movimento do planeta descrevendo a órbita elíptica, mas
, variam com o movimento do planeta descrevendo a órbita elíptica, mas ![]() não varia.
não varia.
Na posição ![]() (afélio) quando o planeta está mais afastado do Sol e na posição
(afélio) quando o planeta está mais afastado do Sol e na posição ![]() (perélio) quando o planeta está mais próximo do Sol, as velocidades nesses pontos são perpendiculares a
(perélio) quando o planeta está mais próximo do Sol, as velocidades nesses pontos são perpendiculares a ![]() , então temos
, então temos ![]() , que nos leva:
, que nos leva:
![]()
Isto significa que ![]() pois
pois ![]() . Quando o planeta orbita o Sol, sua velocidade vai aumentando conforme ele vai
. Quando o planeta orbita o Sol, sua velocidade vai aumentando conforme ele vai ![]() para
para ![]() e diminui quando vai de
e diminui quando vai de ![]() para
para ![]() .
.







