Até o momento estão trabalhando na mecânica clássica em que as velocidades dos corpos são muito menores que a velocidade da luz. Então o que acontece com as leis de conservação se a velocidade dos corpos forem próximas à velocidade da luz, como por exemplo a velocidade do elétron que corresponde a ![]() da velocidade da luz ou estiverem em referenciais diferentes?
da velocidade da luz ou estiverem em referenciais diferentes?
Para responder essa pergunta devemos avançar na relatividade especial de Einstein, na qual contém conceitos referentes a equação de transformação de Lorentz que podem ser encontradas no site Relatividade Restrita.
As leis da Física dever permanecer inalteradas sob qualquer transformação da equação de Lorentz, então é preciso generalizar as leis de Newton e a definição de momento linear para se adaptarem ao princípio da relatividade.
Iremos considerar ![]() para a velocidade da luz,
para a velocidade da luz, ![]() para a velocidade da partícula e
para a velocidade da partícula e ![]() para a velocidade do referencial. Temos que
para a velocidade do referencial. Temos que ![]() e
e ![]() , ou seja nenhuma velocidade será maior que a velocidade da luz.
, ou seja nenhuma velocidade será maior que a velocidade da luz.
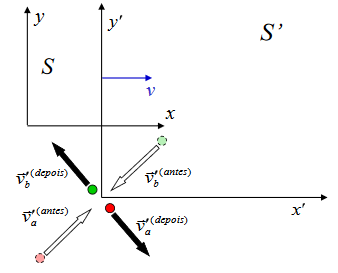
Vamos considerar um modelo (sistema isolado) de duas partículas que colidem em um referencial ![]() , no qual o momento linear é conservado. Temos então que o momento antes da colisão é igual ao momento depois da colisão.
, no qual o momento linear é conservado. Temos então que o momento antes da colisão é igual ao momento depois da colisão.
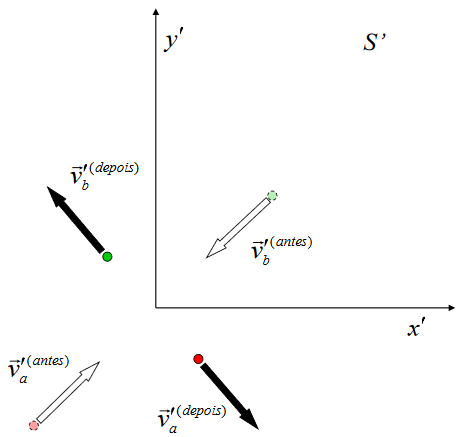
Em um outro referencial ![]() , no qual aplicamos a equação de transformação de Lorentz, o momento
, no qual aplicamos a equação de transformação de Lorentz, o momento ![]() não é conservado. Esse resultado viola um dos postulados de Einstein:
não é conservado. Esse resultado viola um dos postulados de Einstein:
Considerando que a equação de transformação de Lorentz está correta, a definição de momento deverá ser reescrita em função da velocidade relativística e termos assim uma equação relativística para o momento de uma partícula de massa ![]() que mantém o princípio da conservação.
que mantém o princípio da conservação.
![Rendered by QuickLaTeX.com \[ \vec{p}=\frac{m\vec{u}}{\sqrt{1-\frac{u^{2}}{c^{2}}}}; \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-7269b561db022b4b824bb2bb79393f2f_l3.png)
Quando ![]() for menor que
for menor que ![]() temos que a razão
temos que a razão ![]() tende a zero e que o denominado se aproxima de
tende a zero e que o denominado se aproxima de ![]() , fazendo com que o momento relativístico se aproxime do momento clássico.
, fazendo com que o momento relativístico se aproxime do momento clássico.
Usando a equação de momento relativístico podemos reescrever a força como:
![]()
A equação preserva a conservação do momento linear quando ![]() tanto na mecânica clássica quanto na relativística em que
tanto na mecânica clássica quanto na relativística em que ![]() tende a zero.
tende a zero.
A seguir iremos fazer a demonstração da conservação do momento
![]()
Usando a fórmula para a transformação de Lorentz das velocidades

- Partícula
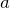
![Rendered by QuickLaTeX.com \[ {v_{ax}}^{antes}=\frac{{v_{x}}^{'}+v}{1+\frac{{v_{x}}^{'}v}{c^{2}}};{v_{ax}}^{depois}=\frac{{v_{x}}^{'}+v}{1+\frac{{v_{x}}^{'}v}{c^{2}}} \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-a03c34106178b4b66bf2e4a5ca2f52f2_l3.png)
- Partícula
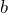
![Rendered by QuickLaTeX.com \[ {v_{bx}}^{antes}=\frac{{-v_{x}}^{'}+v}{1-\frac{{v_{x}}^{'}v}{c^{2}}};{v_{bx}}^{depois}=\frac{{-v_{x}}^{'}+v}{1-\frac{{v_{x}}^{'}v}{c^{2}}} \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-bfc726b70ea99ff412a7c00ece4abc82_l3.png)
Analisando o eixo y temos:
- Partícula
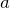
![Rendered by QuickLaTeX.com \[ {v_{ay}}^{antes}=\frac{\sqrt{1-\beta ^{2}}{v_{y}}^{'}}{1+\frac{{v_{x}}^{'}v}{c^{2}}};{v_{ay}}^{depois}=\frac{-\sqrt{1-\beta ^{2}}{v_{y}}^{'}}{1+\frac{{v_{x}}^{'}v}{c^{2}}} \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-2e4a52dcb16f98b833417af59c5c4db5_l3.png)
- Partícula
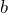
![Rendered by QuickLaTeX.com \[ {v_{by}}^{antes}=\frac{-\sqrt{1-\beta ^{2}}{v_{y}}^{'}}{1-\frac{{v_{x}}^{'}v}{c^{2}}};{v_{by}}^{depois}=\frac{\sqrt{1-\beta ^{2}}{v_{y}}^{'}}{1-\frac{{v_{x}}^{'}v}{c^{2}}} \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-534eed11b111098e4f7b7b57e1282678_l3.png)
Analisando o momento em cada eixo temos:
- eixo x
![]()
- eixo y
![]()
As equações acima mostram que o momento total não foi conservado, ou seja, não ocorre conservação de momento linear. Mas, pode – se mostrar que o momento total será uma quantidade conservada se definirmos o momento usando o fator de Lorentz:
![Rendered by QuickLaTeX.com \[ \vec{p}=\gamma m_{0}\vec {v}=\frac{m_{0}\vec{v}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}; \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-350ed773f56a6869fef1cb1e18139f96_l3.png)
em que ![]() é a massa da partícula no referencial em que se mantém em repouso.
é a massa da partícula no referencial em que se mantém em repouso.
A massa relativística pode ser determinada assim:
![Rendered by QuickLaTeX.com \[ m\vec {v}=\gamma m_{0}\vec {v}\rightarrow\ m=\frac{m_{0}}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-4a118e03c4c1a63000d8d76d99a06c43_l3.png)







