Movimento de Objetos Extensos
Até agora, analisamos a energia, o momento linear e o movimento em si, sem levar em conta as dimensões dos corpos envolvidos. Exceto quando falamos de colisões bidimensionais, quando o tamanho, por exemplo, é importante, para quantificarmos o parâmetro de impacto, ignoramos as dimensões do corpo.
Contudo, na vida real observamos que corpos ou objetos possuem dimensões físicas, como comprimento, largura, espessura, etc.
Como podemos ignorar essas dimensões e considerar o corpo/objeto como sendo um “ponto material”?
A resposta depende do tipo de problema que está tratando. Para calcular a velocidade de uma bola de futebol no solo, quando ela cai de uma altura de 20 m, evidentemente as dimensões da bola são irrelevantes para uma primeira aproximação da sua velocidade.
No entanto, para cálculos precisos, é preciso considerar a sua dimensão, pois entre outras coisas, é importante saber se a bola desce girando ou não.
Nós falaremos de rotação de um corpo na página sobre a conservação do momento angular. Vamos nos concentrar aqui a discutir o movimento de translação do corpo.
No caso da bola, apesar de ser um corpo extenso, dá para analisar facilmente o seu movimento de translação. E também não é difícil imaginá-la como sendo um “ponto material”.
No entanto, vamos analisar no vídeo abaixo o movimento de um outro objeto bem familiar: a vassoura.
O vídeo mostra que o movimento da vassoura é bastante complexo – trata-se de uma mistura de rotação com translação e que em princípio, parece que não conseguimos matematizar o seu movimento.
No entanto, se analisarmos o movimento atentamente, vemos que um ponto da vassoura executa um movimento bem mais simples que dos outros pontos da vassoura. Esse ponto é chamado de centro de massa.
De fato, o centro de massa descreve uma trajetória parabólica. Trata-se um movimento semelhante ao lançamento de projéteis: ele ocorre num plano vertical, com a componente vertical da velocidade sendo constante e a componente vertical acelerada, por conta da força da gravidade.
Embora seja um pouco mais difícil perceber, a vassoura gira em torno do centro de massa, ao mesmo tempo em que ele se move como uma partícula pontual.
No caso da vassoura, é fácil localizar o seu centro de massa: basta encontrar o ponto da vassoura que fica em equilíbrio, ao tentar equilibrá-la com um dedo.
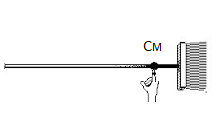
É claro, há uma questão importante a ser respondida: por que a vassoura fica em equilíbrio na situação acima? Essa pergunta pode ser respondida ao estudarmos a estática de um objeto extenso, que envolve o conceito de torque, a ser abordado na página sobre momento angular.
Como a distribuição da massa da vassoura não é uniforme por conta de uma massa maior das cerdas, o centro de massa estará mais próximo delas. Se tentarmos equilibrar a vassoura fora desse ponto ela rotacionará.
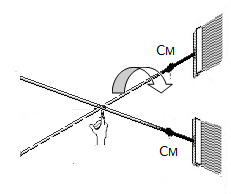
É claro, utilizar o equilíbrio é apenas um método simples de encontrar o centro de massa de um corpo. Há situações complexas onde esse método é totalmente inviável.
Na próxima seção, vamos dar uma definição matemática do centro de massa e como obtê-lo.
O Centro de Massa
Para entender matematicamente o conceito de centro de massa, começaremos analisando um sistema formado por duas partículas pontuais. Em seguida, estenderemos para sistemas com várias partículas, culminando com objetos extensos, que possuem uma distribuição contínua de massa.
Considere um sistema formado por duas partículas, conforme mostra a figura abaixo. Para encontrarmos a posição do centro de massa, temos que conhecer as posições dos corpos 1 e 2, assim como as suas massas.
Para identificarmos a posição de centro de massa, primeiro vamos definir a origem ![]() do nosso sistema de coordenadas.
do nosso sistema de coordenadas.
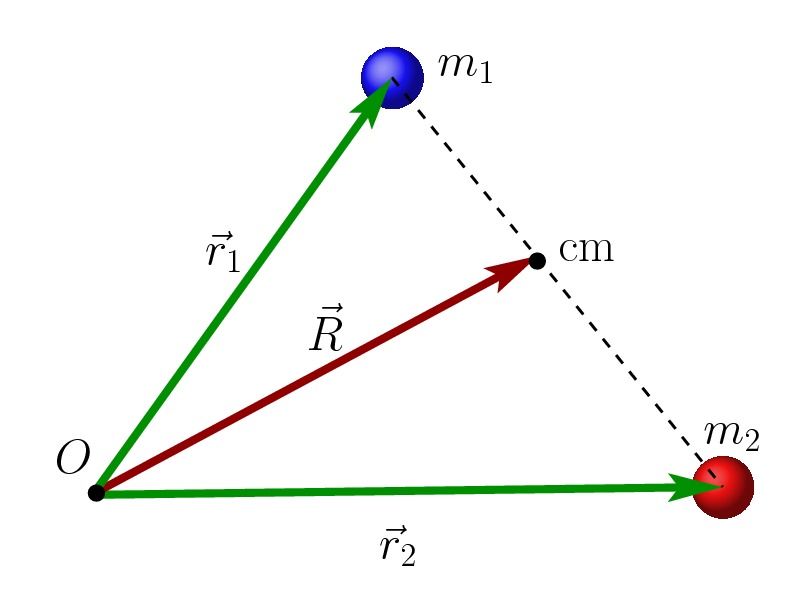
Para a escolha de ![]() na figura acima, o vetor posição do corpo 1, de massa
na figura acima, o vetor posição do corpo 1, de massa ![]() , é dado por
, é dado por ![]() . Similarmente, temos o vetor posição
. Similarmente, temos o vetor posição ![]() para o corpo 2, de massa
para o corpo 2, de massa ![]() .
.
O centro de massa desse sistema é dado pelo vetor posição
![]()
onde ![]() é a massa total do sistema.
é a massa total do sistema.
Para entendermos por que a equação acima dá a posição de centro de massa desse sistema, vamos analisar a dinâmica envolvendo esse sistema.
Vamos supor que uma força externa ![]() atue sobre esse sistema. Por exemplo, a força da gravidade.
atue sobre esse sistema. Por exemplo, a força da gravidade.
Como forças internas se anulam, temos que a força externa é a força resultante sobre o sistema:
![]()
Pela 2ª Lei de Newton,
![]()
onde ![]() e
e ![]() a aceleração do sistema, que a identificaremos como sendo a aceleração do centro de massa.
a aceleração do sistema, que a identificaremos como sendo a aceleração do centro de massa.
Por outro lado, a força resultante é a soma (vetorial) das forças sobre as partículas ![]() e
e ![]() que compõem o sistema:
que compõem o sistema:
![]()
onde novamente pela 2ª Lei de Newton,
![]()
Temos portanto que
![]()
Mas o vetor aceleração é igual a derivada do vetor velocidade, que por sua vez é derivada do vetor posição, ou seja,
![]()
Segue portanto que
![]()
ou seja,
![]()
O resultado acima mostra que para um objeto extenso sob ação de uma força externa resultante, a sua dinâmica se resume na ação dessa força sobre um ponto, justamente o centro de massa, onde podemos concentrar toda a massa do objeto. Temos portanto que
Não seria surpresa, portanto, que o centro de massa da vassoura do vídeo acima irá descrever uma trajetória parabólica se ela estiver sob ação da força gravitacional.
Podemos estender a definição para a uma situação mais geral em que ![]() partículas estão situadas em diferentes pontos no espaço. Neste caso a massa total é
partículas estão situadas em diferentes pontos no espaço. Neste caso a massa total é ![]() e a posição do centro de massa é dada por:
e a posição do centro de massa é dada por:
![Rendered by QuickLaTeX.com \[ \vec{R}=\frac{ m_1\vec{r}_1+m_2\vec{r}_2+m_3\vec{r}_3+\ldots + m_N \vec{r}_N}{M} = \frac{1}{M}\sum_{i=1}^{N}m_i \vec{r}_i \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-594eea9ddcc38bb29bd44da1259aab1b_l3.png)
Em coordenadas cartesianas, o vetor ![]() possui componentes nas direções
possui componentes nas direções ![]() e
e ![]() . Logo, podemos escrever o vetor posição do centro de massa em termos das componentes
. Logo, podemos escrever o vetor posição do centro de massa em termos das componentes ![]() e
e ![]() .
.
Explicitamente, usando as coordenadas cartesianas, ![]() têm componentes
têm componentes ![]() e
e ![]() . Logo,
. Logo,
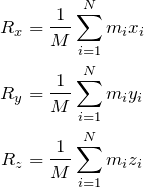
Exemplo 1: centro de massa de quatro partículas nos vértices de um quadrado
Para ilustrar melhor as últimas fórmulas dadas, vamos calcular o centro de massa de quatro partículas posicionadas nos vértices de um quadrado de lado ![]() , sendo duas de massa
, sendo duas de massa ![]() e duas de massa
e duas de massa ![]() . As partículas mais pesadas estão localizadas num mesmo lado do quadrado
. As partículas mais pesadas estão localizadas num mesmo lado do quadrado
A figura abaixo à esquerda mostra o sistema com as quatro partículas, onde já fizemos a nossa escolha do sistema de coordenadas.
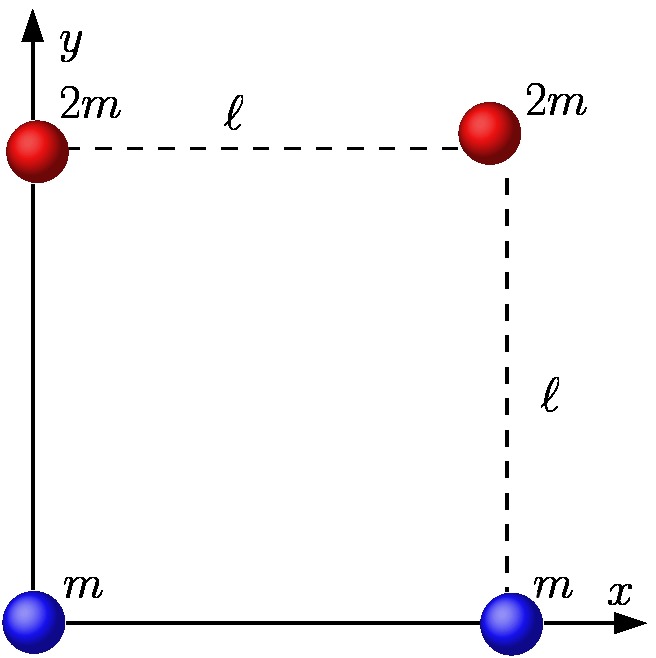
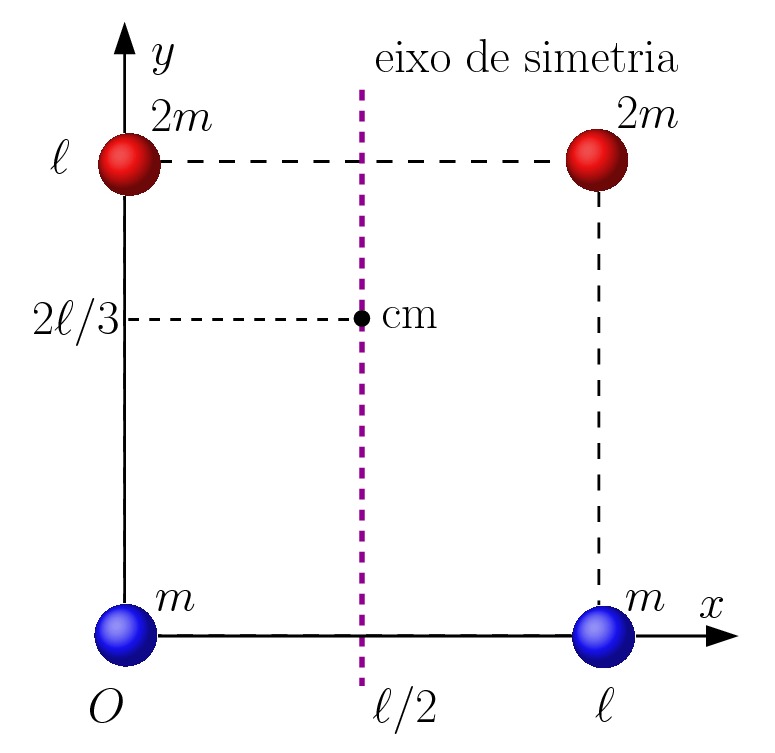
De acordo com essa escolha do sistema de coordenadas, temos que
![]()
Como ![]() e
e ![]() , temos que
, temos que
![]()
Para a componente ![]() ,
,
![]()
e como ![]() e
e ![]() , obtemos
, obtemos
![]()
Como os corpos estão no plano ![]() , temos que
, temos que
![]()
Observe na figura à direita acima que ![]() se localiza num ponto sob o eixo vertical, que é o eixo de simetria da distribuição das massas (o lado esquerdo é espelho do lado direito). É resultado geral de que se o objeto apresenta alguma simetria na distribuição de massas, que pode ser um ponto ou uma linha, o centro de massa vai estar localizada nesse ponto ou linha de simetria.
se localiza num ponto sob o eixo vertical, que é o eixo de simetria da distribuição das massas (o lado esquerdo é espelho do lado direito). É resultado geral de que se o objeto apresenta alguma simetria na distribuição de massas, que pode ser um ponto ou uma linha, o centro de massa vai estar localizada nesse ponto ou linha de simetria.
Observa-se que a componente ![]() no centro de massa,
no centro de massa, ![]() , está a um terço dos corpos de massa
, está a um terço dos corpos de massa ![]() , ou seja, mais perto de onde há mais massa.
, ou seja, mais perto de onde há mais massa.
Centro de massa de corpos maciços
Desde que saibamos onde se localizam as partículas constituintes de um sistema, assim como as suas respectivas massas, podemos encontrar a posição do seu centro de massa calculando-se ![]() e
e ![]() .
.
No entanto, como calcular um objeto ou corpo de um objeto extenso? Ou seja, há uma distribuição contínua de partículas que constituem esse sistema do ponto de vista macroscópico. Por exemplo, como calcular o centro de massa da vassoura do vídeo mostrado acima?
Nós podemos adaptar as expressões para ![]() e
e ![]() para esses objetos, fazendo-se uso dos conceitos de cálculo diferencial e integral.
para esses objetos, fazendo-se uso dos conceitos de cálculo diferencial e integral.
A ideia já foi exposta algumas vezes. Vamos partir de algo que conhecemos, que no caso, o cálculo de centro de massa de partículas granulares.
Podemos imaginar que um objeto extenso, de massa ![]() , que possui uma distribuição contínua de massa, é na verdade formado por um número
, que possui uma distribuição contínua de massa, é na verdade formado por um número ![]() muito grande de partículas granulares, muito próximas entre si, cada uma com massa
muito grande de partículas granulares, muito próximas entre si, cada uma com massa ![]() .
.
A componente ![]() do centro de massa será
do centro de massa será
![Rendered by QuickLaTeX.com \[ R_x=\frac{1}{M} \sum_{i=1}^N x_i \Delta x_i \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-f55f8ca3142f70c77bfafc64c9199cee_l3.png)
No limite em que ![]() tende a zero, trocamos
tende a zero, trocamos ![]() por
por ![]() , a massa infinitesimal (massa muito pequena) e a somatória se torna uma integral:
, a massa infinitesimal (massa muito pequena) e a somatória se torna uma integral:
![]()
Analogamente, para as componentes ![]() e
e ![]() ,
,
As equações acima são meramente formais. É preciso conhecer como a massa é distribuída no objeto, ou seja, é preciso conhecer a sua densidade de massa; massa por unidade de volume, para um corpo volume. Para um corpo de espessura desprezível, usamos a densidade superficial e para um corpo extenso e delgado, usamos a densidade linear.
Exemplo 2: centro de massa de uma barra delgada e uniforme
Vamos calcular neste exemplo o centro de massa de uma barra delgada, de comprimento ![]() e massa
e massa ![]() uniformemente distribuída.
uniformemente distribuída.
Neste caso, temos uma densidade linear de massa:
![]()
Como a massa está uniformemente distribuída,
![]()
Vamos colocar a barra ao longo do eixo ![]() , fazendo com que a origem
, fazendo com que a origem ![]() do eixo
do eixo ![]() coincida com uma extremidade da barra. Assim, a outra fica na posição
coincida com uma extremidade da barra. Assim, a outra fica na posição ![]() , conforme mostra a figura abaixo:
, conforme mostra a figura abaixo:
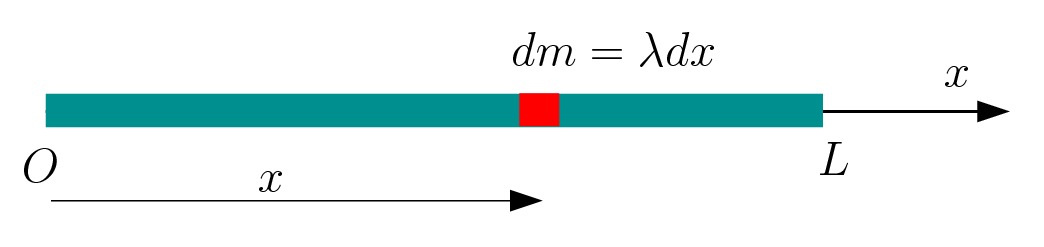
Neste caso, como não há distribuição e massa ao longo dos eixos ![]() e
e ![]() ,
,
![]()
conforme esperado, o centro de massa estará sobre o eixo ![]() , em cima da barra. Temos que
, em cima da barra. Temos que
![]()
onde na segunda igualdade usamos que ![]() (
(![]() , neste caso).
, neste caso).
A integral dá ![]() , portanto
, portanto
![]()
ou seja, o centro de massa de uma barra uniforme está localizado no meio dela.
Evidentemente, este resultado é um tanto esperado. Conforme observação feita no Exemplo 1 envolvendo distribuição de partículas granulares, podemos explorar aqui a simetria da distribuição de massa de um objeto extenso.
Se a distribuição apresentar alguma simetria, não há necessidade de se fazer o cálculo de uma ou mais componentes da posição do centro de massa.
Como exemplos, vamos discutir qualitativamente onde se localiza o centro de massa de alguns objetos que possuem alguma simetria de distribuição de massa.
No caso de uma esfera maciça homogênea, ela possui simetria radial e portanto o centro de massa fica no centro da esfera.
O centro de massa de um cilindro contendo um líquido homegêneo possui simetria cilíndrica. Isto significa que o centro de massa está localizado num ponto sob o eixo vertical, que passa pelo centro do cilindro (o eixo principal do cilindro). A medida que se adiciona líquido ao cilindro, o centro de massa do sistema vai subindo verticalmente.
Similarmente ao cilindro, um cone de trânsito homogêneo também possui simetria ao longo do eixo vertical, que passa no meio do cone. Logo, o seu centro de massa se localiza em um ponto ao longo desse eixo.

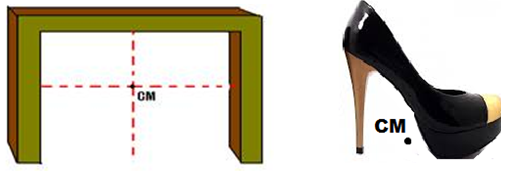
Um outro aspecto muito importante do centro de massa de um objeto é que, embora a primeira vista imaginamos que o centro de massa está no interior do objeto, isso não é verdade.
Nos dois exemplos abaixo, o centro de massa se encontra fora do objeto.
Centro de massa de Objetos Compostos
Conforme discutido acima, o centro de massa de um objeto está relacionado à simetria de distribuição de massa dele. Quando a simetria é em relação a um ponto, o centro de massa está localizado nesse ponto; se a simetria for um eixo, o centro de massa estará nesse eixo.
Existem situações em que aparentemente o objeto como um todo não possui distribuição simétrica de massa. Contudo, se analisarmos com cuidado, veremos que esse objeto pode ser dividido mentalmente em dois ou mais pedaços, sendo que para cada pedaço há uma simetria e portanto pode-se localizar o centro de massa. Com isto, reduzimos o nosso problema em um sistema com duas ou mais partículas pontuais: cada centro de massa se comporta como uma dessas partículas.
Se conhecermos as posições dessas “particulas” e as suas massas, podemos calcular facilmente o centro de massa do objeto como um todo usando a fórmula
![Rendered by QuickLaTeX.com \[ \vec{R} = \frac{1}{M} \sum_{i=1}^N m_i \vec{r}_i \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-f51e87d0dfd76128b0ced2c603224d32_l3.png)
onde ![]() é a quantidade de “partículas”, ou seja, o número de objetos divididos mentalmente.
é a quantidade de “partículas”, ou seja, o número de objetos divididos mentalmente.
Para ilustrar, vamos aplicar essa técnica para encontrar o centro de massa de uma vassoura.
Exemplo 3. O centro de massa de uma vassoura
Vamos calcular o centro de massa da vassoura, representada na figura abaixo. Para isto, observamos que ela pode ser dividida em três partes, onde para cada parte conhecemos as dimensões e as massas. Pela simetria, o centro de massa da vassoura deve estar sob um eixo que passa no interior do cabo. Chamaremos esse eixo de eixo ![]() .
.
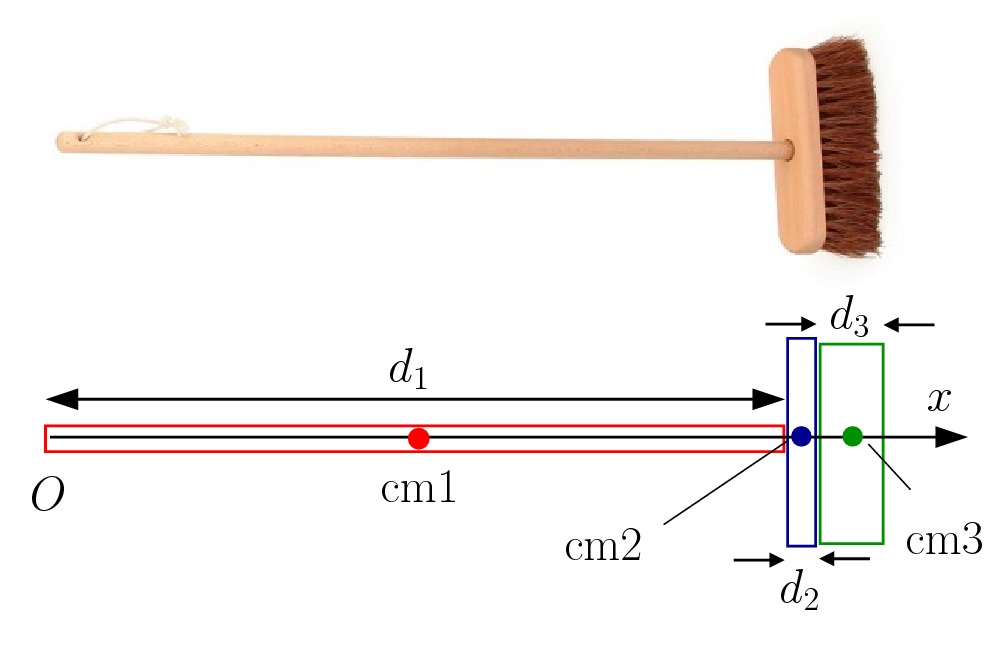
Vamos supor que as partes possuem comprimento ao longo do eixo ![]() de
de ![]() e
e ![]() , com as massas
, com as massas ![]() e
e ![]() , respectivamente.
, respectivamente.
Colocando a origem do eixo ![]() na extremidade do cabo sem as cerdas, temos que os centros de massa de cada componente da vassoura são
na extremidade do cabo sem as cerdas, temos que os centros de massa de cada componente da vassoura são
![]()
As únicas suposições assumidas para a equação acima são que em cada componente da vassoura a distribuição de massa e a espessura são uniformes. Daí, o centro de massa de cada componente estará localizado no seu centro.
Com isto, o centro de massa da vassoura é dado por
![]()
onde ![]() é a sua massa total.
é a sua massa total.
Substituindo os valores de ![]() e
e ![]() dados acima, obtemos
dados acima, obtemos
![]()
Evidentemente, ![]() é maior do que
é maior do que ![]() , que é o centro do cabo, conforme esperado. Logo, o centro de massa da vassoura encontra-se mais próximo das cerdas.
, que é o centro do cabo, conforme esperado. Logo, o centro de massa da vassoura encontra-se mais próximo das cerdas.
Conservação do Momento Linear e o Centro de Massa
Vamos considerar o sistema com duas partículas pontuais, de massas ![]() e
e ![]() , onde
, onde ![]() permanece constante. Se uma força externa
permanece constante. Se uma força externa ![]() atua sobre esse sistema, temos que
atua sobre esse sistema, temos que
![]()
onde ![]() é a aceleração do centro de massa, conforme já discutido acima.
é a aceleração do centro de massa, conforme já discutido acima.
Se ![]() , temos que
, temos que
![]()
ou seja, como a massa é constante, a aceleração do centro de massa deve ser zero, portanto a sua velocidade deve ser constante. Se definirmos
![]()
como o momento linear do centro de massa, observamos que
![]()
ou seja, o momento linear total do sistema é igual ao momento linear do centro de massa. Esse raciocínio pode ser generalizado por um sistema de ![]() partículas.
partículas.
Temos portanto que para um sistema com ![]() corpos, a 2ª Lei de Newton fica
corpos, a 2ª Lei de Newton fica
![Rendered by QuickLaTeX.com \[ \vec{F}_\textrm{ext} = \frac{d\vec{P}}{dt} = \frac{d}{dt} \left( \sum_{i=1}^N \vec{p}_i \right) \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-3bb312b8e9ad2697e57a7e226c3cce22_l3.png)
Se a força resultante externa for nula, ![]() , o momento linear do centro de massa, que é também o momento total do sistema, será constante, um resultado que já exploramos exaustivamente.
, o momento linear do centro de massa, que é também o momento total do sistema, será constante, um resultado que já exploramos exaustivamente.

Na próxima página iremos discutir a conservação de massa para um sistema de massa variável.
Ir para a próxima seção: Conservação de Momento Linear para um sistema de massa variável.







