Colisões
Em física, entendemos como processo de colisão a interação entre dois ou mais corpos, inicialmente livres (ou seja, não há interação entre eles). Como consequência, há alteração do estado final desses corpos, como a velocidade.
Do ponto de vista clássico, os corpos que resultam da colisão são os mesmo que iniciaram, como colisões entre duas bolas de bilhar.

Conforme veremos mais adiante, como as bolas se movem livremente sobre um plano (a mesa do bilhar), trata-se de uma colisão bidimensional. O objeto a ser lançado é chamado de projétil e aquele que se encontra inicialmente em repouso, o alvo.
Até este ponto, o significado dos termos físicos coincidem com o nosso entendimento dessas palavras no cotidiano.
Na próxima seção, nos dedicaremos a discutir a cinemática das colisões que ocorrem entre partículas, como as colisões entre prótons que ocorrem no LHC (Large Hadron Collider), o colisor de partículas localizado no laboratório do CERN. Como os prótons iniciais são extremamente energéticos, estão com velocidades muito próximas à da luz. Por conta disto, colisões no LHC são descritos utilizando-se a teoria da relatividade restrita.
Uma outra peculiaridade que ocorre em colisões na escala subatômica é que partículas iniciais que participam da colisão podem simplesmente desaparecer e outras surgirem em seu lugar. Se lembrarmos da seção energia relativística, vimos que dentro da teoria da relatividade restrita a transformação de partículas é possível, como o decaimento do nêutron livre, que se transforma em próton, elétron e o antineutrino do elétron. Além disto, por causa da equivalência massa – energia, a massa pode não se conservar numa colisão subatômica.
De uma forma bem geral, as seguintes observações podem ser feitas num processo de colisão:
- a energia cinética do sistema se conserva em algumas colisões; em outras, não;
- em colisões clássicas, a massa total do sistema se conserva, mas não necessariamente em uma colisão na escala subatômica;
- os corpos que participam inicialmente da colisão podem desaparecer, dando origem a novos corpos.
- por colisão, nem sempre há o contato entre os corpos; os prótons do LHC não se encostam, como dá a entender a palavra “colisão”.
A lista não termina aí, mas ela já é suficiente para perguntarmos: o que caracteriza uma colisão em física?
De uma forma geral, podemos fazer a seguinte definição:
É importante enfatizar que por interação entendemos como a ação de forças internas que formam pares de forças do tipo ação – reação. Têm uma intensidade bastante grande e conforme especificado, atuam por um tempo muito curto. No caso clássico, essas forças ocorrem via contato entre os corpos. É o que ocorre com as bolas de bilhar. No caso de partículas, podemos considerar, por exemplo, forças coulombianas entre duas partículas carregadas. Se forem muito pequenas, como dois prótons, haverá a repulsão entre elas, sem jamais se encostarem.
No caso do LHC, como os prótons são muito energéticos, eles conseguem ficar muito próximos uns dos outros. Neste caso, a força coulombiana é irrelevante e forças intensas de curto alcance (forças forte e fraca) começam a ficar mais importantes. Dependendo da energia, há a probabilidade desses prótons serem “quebrados” e novas partículas surgirem. Essa quebra não ocorre via contato entre os prótons.
Em todos esses fenômenos, do micro ao macro, a interação só envolve forças internas, ou seja, ![]() numa colisão e consequentemente o momento linear total se conserva.
numa colisão e consequentemente o momento linear total se conserva.
Numa colisão clássica entre dois corpos, podemos classificá-la de acordo com a conservação (ou não) da energia cinética total dos corpos:
a. Colisão elástica. Neste tipo de colisão, a energia cinética total é conservada. Por conta da conservação da energia cinética, não há a deformação dos corpos (é preciso gastar energia para deformar um corpo!).
b. Colisão inelástica. A energia cinética total não é conservada. Há um caso extremo de colisão inelástica, onde os corpos são grudados um no outro, chamado de colisão perfeitamente inelástica.
Para classificar esses tipos de colisões, Newton introduziu o chamado coeficiente de restituição, ![]() , que discutiremos a seguir.
, que discutiremos a seguir.
Coeficiente de restituição
O coeficiente de restituição ![]() é um conceito que facilita o estudo quantitativo das colisões.
é um conceito que facilita o estudo quantitativo das colisões.
Numa colisão unidimensional, ele é definido como sendo a razão entre o módulo da velocidade relativa de afastamento (depois da colisão) e o módulo da velocidade relativa de aproximação (antes da colisão).
Se ![]() e
e ![]() são respectivamente as velocidades das partículas 1 e 2 antes da colisão e
são respectivamente as velocidades das partículas 1 e 2 antes da colisão e ![]() e
e ![]() após a colisão, temos que
após a colisão, temos que
![]()
Por ser definido como uma razão entre os módulos das velocidades é uma grandeza adimensional e positiva.
Para cada tipo de colisão temos um valor de ![]() . Vamos mostrar a seguir que
. Vamos mostrar a seguir que
a. ![]() para a colisão elástica;
para a colisão elástica;
b. ![]() para a colisão inelástica. No caso de uma colisão perfeitamente inelástica,
para a colisão inelástica. No caso de uma colisão perfeitamente inelástica, ![]() .
.
É fácil ver que ![]() numa colisão perfeitamente inelástica, pois como os corpos saem grudados,
numa colisão perfeitamente inelástica, pois como os corpos saem grudados, ![]() e consequentemente pela equação acima,
e consequentemente pela equação acima, ![]() .
.
Vamos discutir em maiores detalhes esses dois tipos de colisão, primeiramente considerando-se apenas as colisões unidimensionais.
Colisão Elástica Unidimensional
Conforme discutido, como se trata de uma colisão, o momento linear total do sistema se conserva. Além disto, numa colisão elástica, a energia cinética também se conserva.
Vamos considerar a colisão entre dois corpos de massas ![]() e
e ![]() , movendo-se na direção horizontal (eixo
, movendo-se na direção horizontal (eixo ![]() ) antes e após a colisão. Sejam
) antes e após a colisão. Sejam ![]() e
e ![]() , as velocidades respectivamente dos corpos 1 e 2 antes da colisão e
, as velocidades respectivamente dos corpos 1 e 2 antes da colisão e ![]() e
e ![]() após a colisão.
após a colisão.
A figura mostra que os corpos 1 e 2 deslocam-se em sentidos opostos, mas ![]() poderia estar se movendo no mesmo sentido (com a condição que evidentemente
poderia estar se movendo no mesmo sentido (com a condição que evidentemente ![]() para que haja a colisão) ou que
para que haja a colisão) ou que ![]() , entre outras possibilidades.
, entre outras possibilidades.

Pela conservação do momento total (soma dos momentos dos corpos antes e após a colisão), temos a seguinte equação:
![]()
Como a energia cinética de um corpo de massa ![]() e velocidade
e velocidade ![]() é
é ![]() , a conservação da energia cinética nos leva à seguinte equação:
, a conservação da energia cinética nos leva à seguinte equação:
![]()
Como temos duas equações, podemos encontrar duas incógnitas. No caso, vamos assumir que as massas das partículas e as velocidades iniciais são conhecidas. Com isto, podemos obter as velocidades finais ![]() e
e ![]() . Trata-se apenas de uma manipulação algébrica envolvendo as equações (1) e (2). Eliminando o fator
. Trata-se apenas de uma manipulação algébrica envolvendo as equações (1) e (2). Eliminando o fator ![]() da Eq. (2) e colocando tudo que depende do corpo 1 à esquerda e do corpo 2 à direita, temos o seguinte sistema:
da Eq. (2) e colocando tudo que depende do corpo 1 à esquerda e do corpo 2 à direita, temos o seguinte sistema:
![Rendered by QuickLaTeX.com \begin{align*} m_1(v_1-v_1') &= m_2(v_2'- v_2) \\[4pt] m_1({v_1}^2 - {v_1'}^2) &= m_2 ({v_2'}^2 - {v_2}^2) \end{align*}](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-9b97a62c3a6a6b0372bd2393afeb0e8d_l3.png)
Observando que ![]() , podemos dividir a segunda equação pela primeira, membro a membro, eliminado-se assim as massas, o que leva a
, podemos dividir a segunda equação pela primeira, membro a membro, eliminado-se assim as massas, o que leva a
![]()
Podemos isolar ![]() da equação acima e substituir na Eq. (1), o que dá
da equação acima e substituir na Eq. (1), o que dá
![]()
Substituindo ![]() acima na Eq. (3), obtemos a velocidade final do segundo corpo:
acima na Eq. (3), obtemos a velocidade final do segundo corpo:
![]()
Subtraindo ![]() por
por ![]() , obtemos
, obtemos
![]()
Logo,
![]()
Assim, mostramos que o coeficiente de restituição é igual a 1 para uma colisão elástica unidimensional.
Com o resultado geral acima para as velocidades finais, podemos considerar algumas situações específicas de colisão unidimensional elástica:
Exemplo 1
Vamos considerar o caso em que o corpo 1 com velocidade ![]() colida frontalmente com um corpo 2, em repouso (
colida frontalmente com um corpo 2, em repouso (![]() ). Caso os dois corpos possuam a mesma massa,
). Caso os dois corpos possuam a mesma massa, ![]() , as equações acima para as velocidades finais dão
, as equações acima para as velocidades finais dão ![]() e
e ![]() .
.
Uma situação prática, cujo resultado acima é facilmente observado, acontece num jogo de bilhar, conforme mostra o vídeo abaixo.
Este resultado também consegue explicar o movimento do pêndulo de Newton. Quando soltamos uma única esfera, ela bate com velocidade horizontal ![]() na próxima. Após sucessivas colisões, a última adquire a velocidade
na próxima. Após sucessivas colisões, a última adquire a velocidade ![]() e a primeira esfera entra em repouso. O raciocínio pode ser aplicado para duas esferas e assim por diante.
e a primeira esfera entra em repouso. O raciocínio pode ser aplicado para duas esferas e assim por diante.
Exemplo 2
Vamos considerar dois corpos de massas diferentes, com velocidades iniciais iguais em módulo, mas opostas: ![]() e
e ![]() . Nesta caso, as velocidades finais que derivamos ficam
. Nesta caso, as velocidades finais que derivamos ficam
![]()
Uma situação interessante ocorre quando uma das massas é muito maior do que a outra, digamos ![]() (leia-se
(leia-se ![]() muito maior do que
muito maior do que ![]() ). Neste caso,
). Neste caso,
![Rendered by QuickLaTeX.com \[ v_1'= \frac{m_1\left(1-\frac{3m_2}{m_1}\right)}{m_1\left(1+\frac{m_2}{m_1}\right)} v \quad \Rightarrow \quad v_1' \approx v \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-e12832c53fecd44ec59a4a780b5f70e6_l3.png)
onde o símbolo “![]() ” se refere a aproximadamente igual, visto que desprezamos os termos
” se refere a aproximadamente igual, visto que desprezamos os termos ![]() em comparação ao valor 1.
em comparação ao valor 1.
De forma análoga, obtemos
![]()
Este resultado pode ser verificado na prática: deixa-se cair uma bola de basquete, com uma bola de tênis logo acima dela. Ao quicar no solo, a velocidade da bola de basquete é invertida e colide com a bola de tênis, ainda descendo. O vídeo abaixo mostra que após a colisão, ambas sobem, mas a bola de tênis ganha uma velocidade muito maior do que a de basquete.
Colisão inelástica Unidimensional
Na colisão inelástica, somente o momento total do sistema se conserva, portanto temos somente a Eq. (1), que a repetiremos aqui:
![]()
Sem uma informação adicional, não conseguimos escrever as velocidades finais em função das velocidades iniciais, mesmo as massas sendo conhecidas.
Há uma situação extrema, que é a colisão perfeitamente inelástica, onde temos a equação extra ![]() , já que nesse tipo de colisão os corpos saem grudados, portanto com a mesma velocidade.
, já que nesse tipo de colisão os corpos saem grudados, portanto com a mesma velocidade.
Da Eq. (1), segue que
![]()
Em tempos passados, este resultado era bastante útil para se determinar a velocidade da bala de uma arma de fogo. O aparato consiste de um pêndulo formado por um pedaço de madeira, de massa conhecida. Ao disparar a arma contra a madeira, a bala fica alojada nela e o conjunto sobe até uma certa altura máxima, que é medida na sequência.
A figura abaixo ilustra a situação descrita.
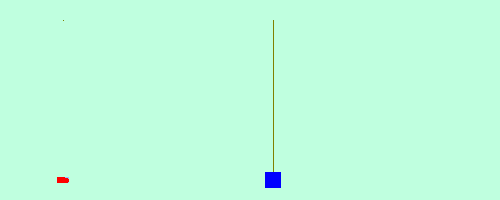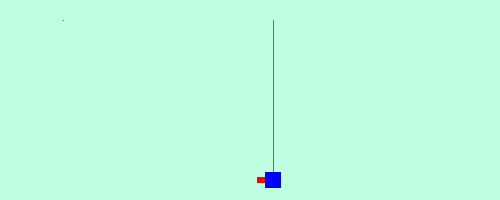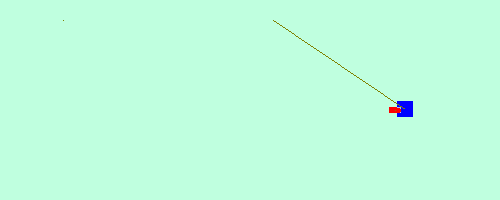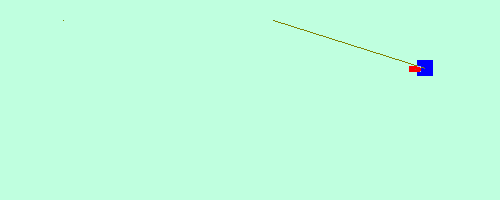
Chamaremos o projétil vermelho de corpo 1 e o pêndulo azul de corpo 2.
Para determinar a velocidade inicial da bala, ![]() , temos que dividir o processo físico mostrado acima em duas etapas:
, temos que dividir o processo físico mostrado acima em duas etapas:
- Primeira etapa: o processo de colisão, quando a bala se aloja no pedaço de madeira.
- Segunda etapa: o sistema formado pela bala alojada e a madeira sobem até atingir uma altura máxima.
A primeira etapa é justamente a colisão perfeitamente inelástica. A velocidade do sistema bala-madeira após a colisão é dada pela Eq. (4), com ![]() (a madeira está inicialmente em repouso):
(a madeira está inicialmente em repouso):
![]()
Na segunda etapa, o sistema bala-madeira, com velocidade ![]() dada acima sobe até atingir uma altura máxima
dada acima sobe até atingir uma altura máxima ![]() . Nesta etapa, podemos utilizar a conservação da energia mecânica, abordada na página Conservação da Energia Mecânica .
. Nesta etapa, podemos utilizar a conservação da energia mecânica, abordada na página Conservação da Energia Mecânica .
Se no ponto mais baixo (ponto A) assumirmos que a energia potencial gravitacional é zero, temos pela conservação de energia que
![]()
onde o ponto ![]() representa o ponto mais alto, onde o sistema para instantaneamente (
representa o ponto mais alto, onde o sistema para instantaneamente (![]() ), para descer em seguida. Temos portanto que
), para descer em seguida. Temos portanto que
![]()
Mas como ![]() , conforme dado acima, temos que
, conforme dado acima, temos que
![]()
Uma importante observação. Na determinação da velocidade inicial da bala, dividimos o processo físico em duas etapas. Por que não usamos somente a conservação de energia? No caso do pêndulo de Newton, a última bola sobe até a altura da primeira bola quando é solta. Logo, verificamos que de fato a energia mecânica se conserva.
O que ocorre se assumirmos a conservação de energia em toda a etapa? Ou seja, inicialmente temos uma bala de massa ![]() e velocidade
e velocidade ![]() , com a madeira em repouso. Na configuração final, temos o sistema bala-madeira com velocidade zero, a uma altura
, com a madeira em repouso. Na configuração final, temos o sistema bala-madeira com velocidade zero, a uma altura ![]() . É certo fazermos
. É certo fazermos
![]()
Neste caso, a velocidade inicial depende de ![]() , ou seja, teríamos encontrado um valor menor do que de fato é. O que está acontecendo?
, ou seja, teríamos encontrado um valor menor do que de fato é. O que está acontecendo?
A resposta é simples: a energia mecânica (neste caso a energia cinética) não se conserva no processo de colisão inelástica. Quando a bala se aloja na madeira, parte da energia cinética da bala se dissipa – no caso, o atrito com a madeira causa um aumento na temperatura do sistema.
Vamos agora discutir colisões cujos corpos participantes não estão restritos a se moverem em uma única dimensão, como a maioria de colisões que ocorre numa mesa de bilhar.
Mas antes, vamos discutir brevemente como definirmos o coeficiente de restituição para colisões bidimensionais
Colisões bidimensionais e coeficiente de restituição
Numa colisão bidimensional, como o próprio nome sugere, o movimento dos corpos ocorrem num plano.
Na colisão unidimensional, definimos o coeficiente de restituição como sendo o módulo da razão entre as velocidades relativas (em relação às velocidades inicias), dada por
![]()
A fórmula acima pode ser aplicada para colisões bidimensionais, mas há a necessidade de se tomar um cuidado; ela só vale para a componente das velocidades ao longo da normal (direção perpendicular) e paralelas ao plano (contato), conforme ilustra a figura abaixo.
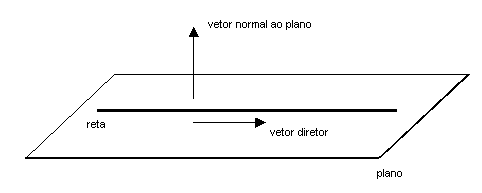
Colisão elástica bidimensional
Quando falamos de colisão elástica bidimensional na física básica, geralmente tratamos um caso particular em que um corpo (projétil) atinge um outro que está inicialmente em repouso (alvo). Na situação final, ambos os corpos possuem velocidades cujas direções não são paralelas à direção da velocidade do projétil.
A animação abaixo mostra esse tipo de colisão que trataremos a seguir. Uma colisão desse tipo ocorre, por exemplo, entre as bolas num jogo de bilhar.
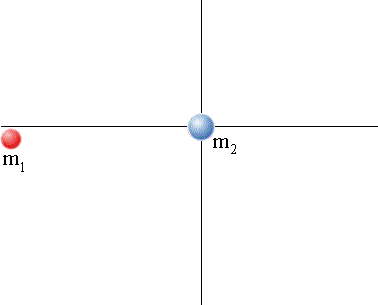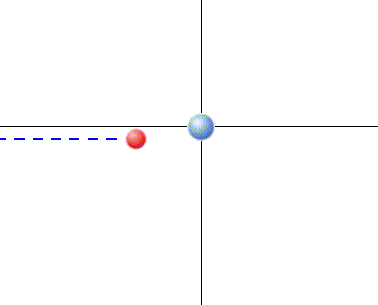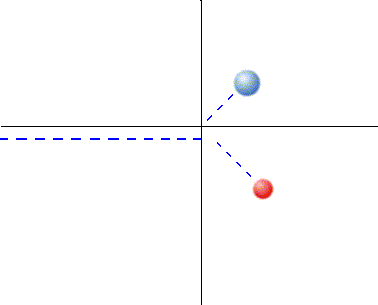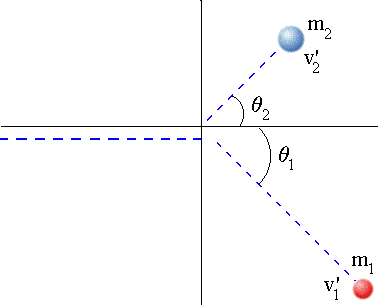
Antes de mais nada, vimos no vídeo acima da colisão frontal entre duas bolas de bilhar, com uma delas em repouso. No caso, a bola inicialmente em repouso (alvo) adquiriu a velocidade da bola que a atingiu (projétil), conforme esperado pela equação de conservação de momento linear em uma dimensão.
Qual a diferença dessa situação com a animação acima, que mostra uma colisão bidimensional? Obviamente, qualquer jogador de bilhar sabe produzir ambas as situações: o resultado do movimento depende da forma como o projétil irá tocar o alvo. Na física, relacionamos a forma como toca com o chamado parâmetro de impacto, cujo símbolo é ![]() . Na situação de baixo estamos considerando a colisão entre as esferas de raios
. Na situação de baixo estamos considerando a colisão entre as esferas de raios ![]() e
e ![]() .
.
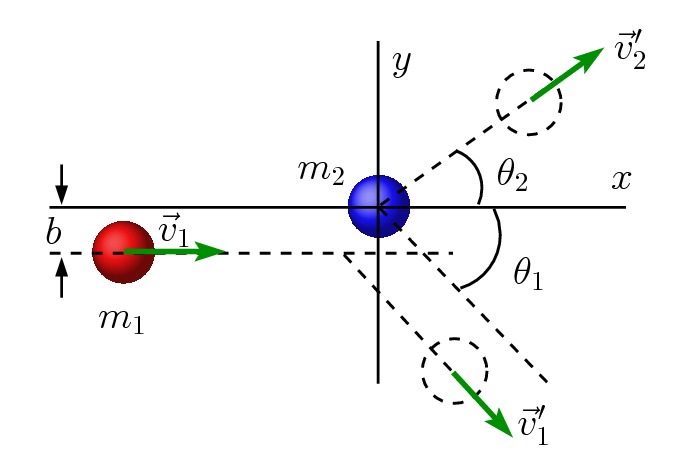
Se ![]() , teremos a colisão frontal e se
, teremos a colisão frontal e se ![]() , evidentemente não haverá colisão.
, evidentemente não haverá colisão.
Vamos a seguir obter as equações envolvidas nesse tipo de colisão, sem nos preocuparmos com o parâmetro de impacto. Assumimos que um dado parâmetro de impacto produziu a situação mostrada na animação.
Em primeiro lugar, como se trata de um processo de colisão, o momento linear total do sistema é conservado, ou seja,
![]()
O importante é lembrar que neste caso, é o vetor momento linear total que se conserva. Utilizando a notação da animação acima, podemos escrever a equação vetorial acima em termos das componentes ![]() e
e ![]() :
:
![Rendered by QuickLaTeX.com \begin{align*} m_1 v_1 &= m_1 v_1' \cos\theta_1 + m_2 v_2'\cos\theta_2 \\[4pt] 0 &= - m_1v_1'\:\textrm{sen}\,\theta_1 + m_2 v_2'\:\textrm{sen}\,\theta_2 \end{align*}](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-59d7fadff6f03217c0fe400f30d3806b_l3.png)
Além das duas equações acima decorrentes da conservação do momento linear, existe uma terceira equação, já que a energia cinética se conserva nas colisões elásticas. Temos que
![]()
Como estamos analisando o caso ![]() , temos que
, temos que
![]()
É importante observar que se as massas ![]() e
e ![]() forem conhecidas, assim como a velocidade
forem conhecidas, assim como a velocidade ![]() , não há como determinar as incógnitas
, não há como determinar as incógnitas ![]() e
e ![]() , visto que só temos três equações.
, visto que só temos três equações.
De qualquer forma, conseguimos tirar uma importante relação entre os ângulos finais quando as massas dos corpos são iguais.
Neste caso, elevando ao quadrado as duas equações vindas da conservação do momento, obtemos:
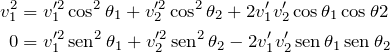
que somando membro a membro, dá
![]()
Por outro lado, a conservação da energia cinética leva à equação
![]()
Juntando essas duas equações e lembrando-se que ![]() , obtemos
, obtemos
![]()
Logo,
![]()
Assim, após uma colisão elástica bidimensional para corpos de mesma massa, com uma delas inicialmente em repouso, os corpos saem em direções perpendiculares.
O coeficiente de restituição é
![]()
Primeiramente, calculamos explicitamente a diferença de vetores ![]() , cujo resultado será um vetor resultante com componentes
, cujo resultado será um vetor resultante com componentes ![]() e
e ![]() . Como queremos o módulo desse vetor, basta somarmos o quadrado da sua componente
. Como queremos o módulo desse vetor, basta somarmos o quadrado da sua componente ![]() com o quadrado da sua componente
com o quadrado da sua componente ![]() e extrair a raiz quadrada. O resultado dá
e extrair a raiz quadrada. O resultado dá ![]() . Logo,
. Logo, ![]() , conforme esperado.
, conforme esperado.
Colisão inelástica bidimensional
Podemos identificar uma colisão inelástica bidimensional, por exemplo em uma batida entre carros, em que a após a colisão os carros passam a se movimentar juntos.

Na animação acima, os carros param porque existe atrito entre a superfície e os veículos e outro carro que serve de obstáculo fazendo que os dois veículos que colidiram inicialmente parem.
Na colisão inelástica bidimensional a conservação do momento linear deve ser expressa fazendo a mesma análise que já foi realizada na colisão elástica bidimensional, isto é, deve-se analisar as componentes dos momentos nas coordenadas ![]() e
e ![]() , antes e depois da colisão.
, antes e depois da colisão.
Com a figura a seguir vamos mostrar que a energia cinética em uma colisão inelástica bidimensional não é conservada, pois ocorre deformação dos copos devido a colisão, ou seja, parte da energia é transferida para os corpos por meio de forças. No entanto ocorre conservação do momento linear.
Sendo a colisão oblíqua, as coordenadas dos vetores na direção ![]() e
e ![]() dos vetores dos momentos, que estão nas mesmas direções dos vetores velocidades são
dos vetores dos momentos, que estão nas mesmas direções dos vetores velocidades são
![]()
![]()
De acordo com a conservação do momento temos:
![]()
pela conservação do momento temos que
![]()
Devido a colisão ser oblíqua a decomposição dos vetores momentos nos dá o desenvolvimento da seguinte equação acima
![]()
![]()
Os dois corpos possuem agora a mesma velocidade, ou seja, ![]() o que nos dá que a velocidade relativa
o que nos dá que a velocidade relativa ![]() .
.
Logo
![]()
Analisando as energia cinética cinética antes e depois da colisão temos que
![Rendered by QuickLaTeX.com \[ \left\{\begin{matrix} K_{1}+K_{2}=\frac{m_{1}v_{1}^{2}}{2}+\frac{m_{2}v_{2}^{2}}{2} & & \\ K_{3}=\frac{m_{3}v_{3}^{2}}{2} \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-540cf7eeef3bca716359bf43f8c43d0b_l3.png)
Com as equações de energia cinética e velocidades verificamos que a energia cinética final ![]() não é igual a energia cinética inicial
não é igual a energia cinética inicial ![]() . Assim temos que a energia cinética não se conserva em uma colisão inelástica bidimensional. Podemos escrever então
. Assim temos que a energia cinética não se conserva em uma colisão inelástica bidimensional. Podemos escrever então
![]()
onde ![]() representa a energia dissipada em alguma outra forma de energia.
representa a energia dissipada em alguma outra forma de energia.
Para entendermos melhor a não conservação de energia do exemplo acima, vamos considerar que as massas dos corpos ![]() e
e ![]() sejam respectivamente dois automóveis de massas iguais a
sejam respectivamente dois automóveis de massas iguais a ![]() e velocidades respectivamente iguais a
e velocidades respectivamente iguais a ![]() e
e ![]() e que
e que ![]() e
e ![]() .
.
Com os ângulos podemos determinar as velocidades e com as velocidades e massa ![]() podemos determinar a energia cinética inicial antes da colisão e a energia cinética final após a colisão.
podemos determinar a energia cinética inicial antes da colisão e a energia cinética final após a colisão.
Substituindo os valores dos ângulos na equação que determina ![]() temos que
temos que
![]()
As energias cinéticas são:
![Rendered by QuickLaTeX.com \[ \left\{\begin{matrix} K_{1}+K_{2}=\frac{1000\times 25^{2}}{2}+\frac{1000\times 50^{2}}{2}=1562,5\times 10^{3}J & & \\K_{3}=\frac{1000\times 25^{2}}{2}=312,5\times 10^{3}J \end{matrix}\right. \]](https://leis-de-conservacao.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-a4e874cbf7bf553be0b90373e8083087_l3.png)
O resultado nos mostra que ocorreu uma perda de energia ![]() .
.
A conservação do momento linear pode ser verificada na simulação abaixo Colisões elásticas e inelásticas.

Na seção Centro de Massa iremos discutir como as dimensões do corpo podem interferir em seu movimento.







